You may have wondered how autograd actually works in imperative programming. In this post, I am going to explain it with hand-by-hand examples. Unlike other tutorials, this post is not borrowing one single line of codes from PyTorch or MXNet, but instead building everything from scratch.

First of all, the term Autograd, or Automatic Differentiation, does not essentially mean calculating the gradients; that should instead be referred to as symbolic differentiation or numerical differentiation. A more precision definition of Autograd should be “automatically chaining the gradients”. Recall the chain rule of differentiation:

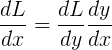
That’s it. Autograd calculates dL/dx from dL/dy if the derivative of y(x) (which we name as a primitive) is implemented. Assume you passed calculus in the freshman year, you now should already have got 80% of Autograd’s idea: chaining the gradients of primitive functions.

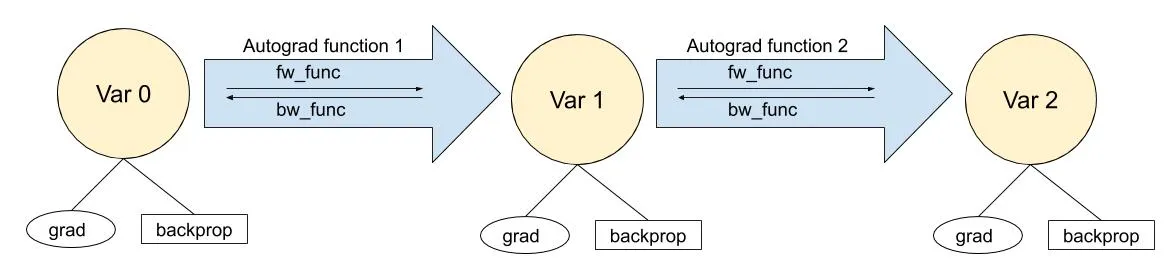
Two basic components of an autograd library: backward-able variables and backward-able functions.

Now let’s delve into the programming part. Throughout this tutorial, we always assume scalar functions—vectorization does not alter the mechanism of autograd. We subclass the float type to add grad attribute and backprop method. We name this new class float_var, the variable of type float.

class float_var(float):
    # Augment float type to add grad, backprop fields
    def __new__(self, value):
        return float.__new__(self, value)

    def __init__(self, value):
        float.__init__(value)
        self.grad = 0.0

    def backprop(self):
        pass

Our first example is for univariate functions. The aforementioned goal is to trace the call order of the forward function (the order of backward funtion will be the reverse) on the fly, and we use Python’s functional programming feature to implicitly record this simple graph. For the univariate case, all it requires is to record the last function call. Super easy, isn’t it? Here is the code:

def autograd_chainer(fw_func, bw_func):
    # Combine a forward function and a backward function into a chain-able autograd function
    def autograd_func(val_in):
        output = fw_func(val_in)
        val_out = float_var(output)
        def backprop_func(self):
            new_grad = bw_func(val_in, val_out, self.grad)
            val_in.grad = new_grad
            val_in.backprop()
        val_out.__setattr__('backprop', types.MethodType(backprop_func, val_out))
        return val_out
    return autograd_func

If you are already familiar with Python decorator, you should find this function similar. It couples a forward function fw_func and a backward function bw_func (both input/output float) and wraps them into an autograd function (input/output float_var).

The output val_out will be registered with a new backprop function that automatically calls the bw_func, multiplied by val_in’s backprop function (recall the chain rule). In this way, all bw_funcs are chained in the reverse order of fw_funcs are called. See full code example at:

[Google Colab notebook]

Notes:

1. When creating a new backward function, we are actually creating a closure (a function plus the environmental variables).
2. We are replacing a class function with a normal function, and types.MethodType makes this substitution process smooth.

Multivariate functions are more complicated and not covered in this post. For full explanation, PyTorch’s notes of autograd mechanism is a good read.